【筆算はするな!】
数学の計算速度を格段にあげる方法

また時間内に解き終わらなかったピヨ...。
テストかな?
そうピヨ...。どうしたらいいピヨ?
そうですね。そしたらまず、ある程度の計算は暗記しちゃいましょう。
...なんと!?
計算速度が遅い原因の一つは計算問題の捉え方を間違えているからです。
ある程度の計算は、頭で考えるより覚えて解いてください。
計算問題は、勉強を続ける限り小中高大とずっとついて回ります。
なので、当然中には「あれ?この式見たことあるな?」というものが出てきます。
それを暗記してしまいましょう!
1. 簡単なたし算ひき算は暗記すべし
ひよこくん。1+1はいくつかな?
それは2ピヨ!
さすがにわかるピヨ!!!
ちなみに今、「1+1」を頭の中で計算したかな?
してないピヨ。してないけどそれくらいわかるピヨ。
「1+1=2」
この計算を私たちがすぐに答えを出せるのは、覚えているからです。
「1+1」って、人生で何百回も出てきますもんね。
同じように、「3+4=7」も、「8+5=13」も覚えているからすぐできるのです。
そうは言っても、どこから暗記すれば良いのかわからないと思います。
いますぐ暗記するべき数式をずばり教えましょう。
たし算ひき算に必要な暗記は、「答えが10になる計算」です。
「1に何を足したら10になるか?」
私たち大人は、すぐにこの答えが9であることが答えられますが、これがポンと出てこないお子さんは暗記ができていません。
次の18個の式は暗記して言えるようにしましょう!

上の式は、右の式も左の式も本質的には同じです。
反射的に答えられるようになるまで何度も声に出したりしながら暗記しちゃいましょう。
2. $11^2$〜$19^2$は暗記!
まずは例題を見てみてください。
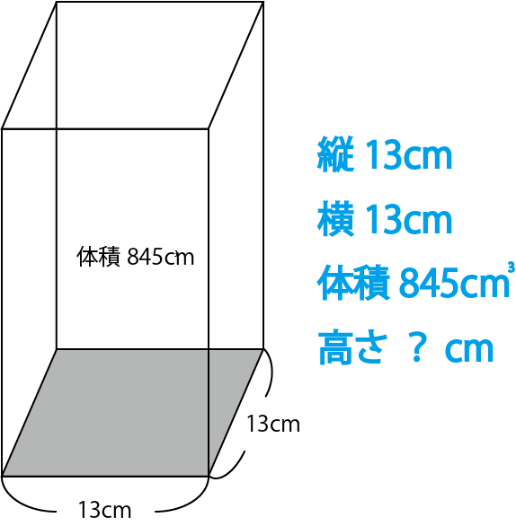
底面が縦13cm、横13cmの正方形で、
体積が $845cm^3$ の四角柱の高さを求めなさい。
この中で暗記で解けるのは「13×13」です。
確かに、よく見かけるピヨね。
11×11とか12×12とかピヨね。
そうです!それを暗記してしまうんです!

これらの式は全て覚えてください!
お、結構あるピヨ...。
もし単純暗記が大変なら、語呂合わせで覚えてしまうと楽ですよ!
覚えてしまえば、最初の問題の底面積(縦13cm,横13cm)は $169cm^2$ とすぐに出せますね。
3. 「とりあえず筆算」はNG!
計算が遅い子の特徴としてもう一つあげられるのが、「すぐに筆算してしまう」という点です。
確かに筆算をした方が早い場合は多いです。
ただ、問題によっては少し工夫するだけで、筆算をすることなく「楽に」「早く」解ける問題もあるんです。
3-1. 498+498ってどう計算する?
ひよこくんならどう計算するかな?
数が半端だから筆算したいピヨ...。
数が半端だし、一見計算しづらそうですよね。すぐ筆算したくなる気持ちもよくわかります。
ただ、計算スピードが早い子は、この問題がちょっとの工夫で筆算せずに解けることを知っています。
まず、「498+498」のそれぞれに「2」を足してあげてください。
すると「500+500」になりますね
「500+500」になれば、暗算でできますね。「500+500=1000」となります。
そして最後に、増やした数分だけ1000から引いてあげてください。
最初にそれぞれ「2」を足したので、合計で「4」増やしました。
なので、「1000ー4=996」となります。
なるほど!半端な数は計算しやすい形に直して計算するピヨね!
そうです!
ただし、最後に必ず足した分はその分引いてあげて、引いた分はその分足してあげてくださいね。
練習問題
※筆算を使わずに解いてみてください。
(1)198+198
答え&解説A. 396
それぞれに2を足して「200+200」にし、答えが「400」です。
400から最初に足した分(それぞれに2を足したので合計で4)を引いてあげます。
「400-4=396」となります。
(2)1998+2997
答え&解説A. 4995
「1998に2」「2997に3」を足して「2000+3000」にします。
すると、答えは5000になります。
そしてここに、増やした分(2+3=5)を引いてあげて「5000-5=4995」となります。
(3)5500+3498
答え&解説A. 8998
3498に2を足して3500にします。
次にそのまま計算します。「5500+3500=9000」
始めに足した「2」を9000から引いて、答えは「8998」となります。
3-2. 98×5ってどう計算する?
お次はかけ算です!
「98×5」ピヨか...。
これはさすがに筆算するピヨ?
...実はこれも筆算なしで解けちゃいます。
な、なんと!!
ここでも、先ほど出てきたテクニックを応用して使っていきます。
まずは、「98」という数字が非常に厄介なので、「2」を足して「100」にしちゃいましょう。
すると「100×5」になりますね。
これは暗算ですぐできますね。答えは「500」です。
最後にそこから、始めに増やした「2」を戻します。
最初に「2」増やしたから、「500ー2」で「498」ピヨか?
んー、惜しい!実は増えてるのは「2」だけではありません!
「2」増やした「100」に「5」をかけているので、始めにたした「2」にも「5」かけられていることに気づいてください。
なので、「500」から「2×5」の「10」を引いてあげてください。
なるほど!すると「500ー10=490」ピヨね!
そういうことです!
練習問題
※筆算を使わずに解いてみてください。
(1)198×8
答え&解説A. 1584
まず、厄介な「198」という数字に2を足して「200」にします。
「200×8=1600」ですね。
最後に、「198」を「200」にして計算したので、余分に増加した分だけ「1600」から引いてあげます。
「1600」から「2×8=16」を引いて、答えは1584となります。
(2)31×30
答え&解説A. 930
まず、31の1が厄介なので、30にしちゃいましょう。
30×30=900となりますね。
最後に、始めに取り除いた1を戻してあげます。
1×30=30を900に足してあげて、答えは930となります。
いかがでしたでしょうか?
計算力というのはとても大事ですが、計算が速い子の多くは、決して考えるのが速いだけではありません
よく出てくる計算の答えを「暗記」していて、かつ「工夫して」計算するすべを知っているからです。
四則演算以外にも、中3で出てくる「展開」「因数分解」は、公式を暗記していくことが重要になってきます。
他にも、問題を解いている中で、覚えておいた方がいいかなと思った計算があれば、ノートに写して暗記していくといいでしょう。
また、計算するときにもすぐに筆算をしたりせず、「これはどう工夫すれば簡単に解けるかな?」と考えて解くことが大事です。
あわせて読みたい
この記事を書いた人

元塾講師・元家庭教師
趣味はラジオを聴くこと
コーディングの勉強がてら
このサイトを作りました