【2分で分かる】箱ヒゲ図って何?世界一わかりやすく解説!

箱ひげ図...わけ分からないピヨーー!!
箱ひげ図のことなら私に任せなさい!
おお...!頼むピヨ!頼むピヨ〜〜〜!
2020年度より中学2年生の教科書に加わったこの「箱ひげ図」。
もともとは高校数学の数学Ⅰで出てくる範囲でした。
なので、みているとはなから「なんか難しそう...」と敬遠している子が非常に多く感じます。
でも、大丈夫!実際は全然大したことはありません。
では、解説を始めていきます!
1. 箱ひげ図とは?
箱ひげ図はズバリ...
データが、
・どれだけ散らばっているか
・どこに偏ってるか
を表す図のことです!
次に各用語とその意味です!
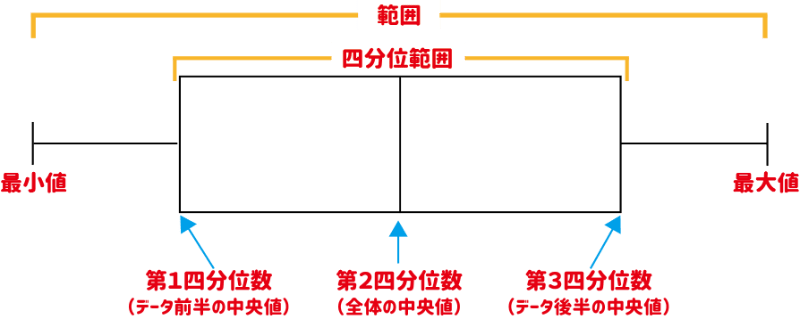
例えば、あるデータの結果が「0,1,2,3,4,5,6,7,8,9,10」だとすると箱ひげ図はこうなります!
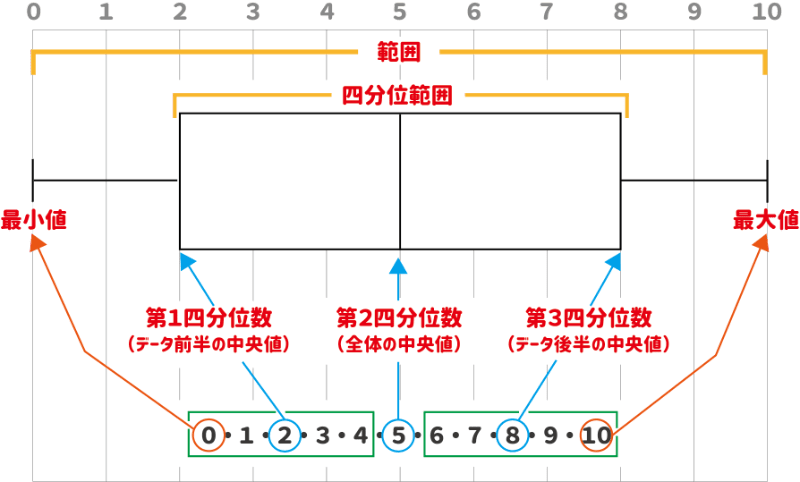
なんとなくイメージはつかめたピヨ!
それでは具体的に用語の解説に移ります!
2. 四分位数と四分位範囲
四分位数(しぶんいすう)とは、データを小さい順に並べたものを4分割にしたときのデータの区切り目のことです。
中でも、
1番目の区切り目を第1四分位数
2番目の区切り目を第2四分位数(中央値)
3番目の区切り目を第3四分位数
と言います。
また、第1四分位数から第3四分位数までの範囲を四分位範囲と言います。
これらを踏まえて改めて箱ひげ図を見てみると

なんとなく見方は分かりましたか?
わかったピヨ!
なんだか数直線に似てるピヨね。
数直線を四分割にしてる感じピヨ。
例えば、1,2,3,4,5の中央値はいくつかな?
真ん中だから...3ピヨ!
正解!
そしたらこれはどうでしょう。
1,2,3,4の中央値はいくつか分かるかな?
真ん中だから...って、真ん中の数字が2と3とふたつあるピヨ。
こういう場合はどうすればいいピヨ?
箱ひげ図はデータの結果が奇数個なら簡単に中央値が取れるのですが、もしデータが偶数個なら普通に考えると中央値が2つになってしまいますね。
例えば、1,2,3,4,の中央値は?と聞かれたら、、、2?3?どっち?どっちも?
ってなると思います。
そういう場合はどうしたらいいのか説明していきます。
3. データが偶数の場合の中央値の取り方
データが偶数個の場合、ズバリ中央にくる2つの値の平均値が中央値になります!
ってことはさっきの1,2,3,4の中央値は2と3平均値の2.5ピヨか!
そゆこと!
他にも例えば、
「1,2,3,4,5,6,7,8,9,10」なら、中央値(第2四分位数)は真ん中の5と6の平均値の5.5となります。
という具合で、真ん中の2つの数字の平均値がデータ全体の中央値になります。
また、第1四分位数と第3四分位数の取り方はこうです!
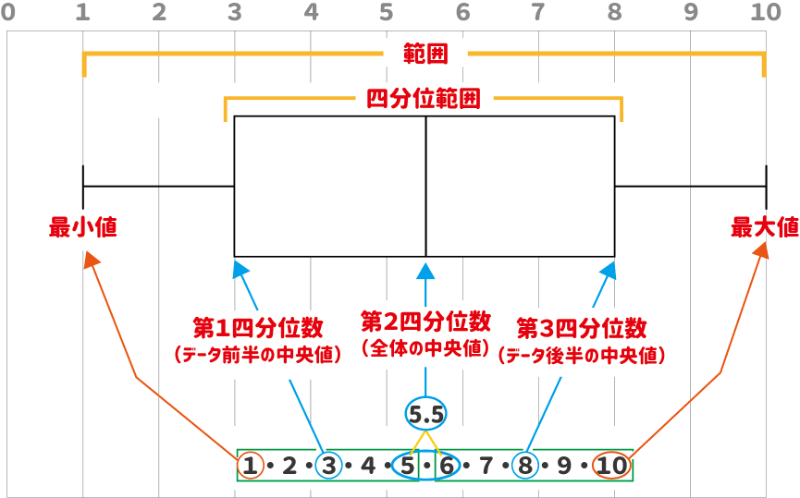
1〜5の中央値「3」が第1四分位数
6〜10の中央値「8」が第3四分位数
となります!
第1四分位数と第3四分位数の値を取る時には、第二四分位数(中央値)は含めずに考えるピヨね!
そう!
あくまで、前半のデータの中央値、後半のデータの中央値と出していくから、ど真ん中の第2四分位数はどちらにも含まず考えるってことです!
まとめです!
【第1四分位数】前半のデータの中央値
【第2四分位数】データ全体の中央値
【第3四分位数】後半のデータの中央値
【四分位範囲】第1〜第3四分位数までの範囲
☆データが偶数個の場合の中央値は、データを小さい順に並べたうちの真ん中の二つの数字の平均値
しっかり復習しましょう!
ピヨ!
あわせて読みたい
この記事を書いた人

元塾講師・元家庭教師
趣味はラジオを聴くこと
コーディングの勉強がてら
このサイトを作りました