【公式一覧】立体の体積・表面積の求め方(円柱・三角柱・円錐・三角錐・球)

体積の公式は何種類もあってわけわからなくなってしまう子が多いです。
ですが、仕組みを知ってしまえば無理して覚えずとも解くことができます。
まずはそれぞれ体積を求める公式をまとめて紹介していきます。
1. 「柱」の体積・表面積の公式

四角柱

三角柱

円柱
柱の体積 = 底面積 × 高さ
表面積 = 底面積 × 2 + 側面積
円周や側面積とかの求め方も知りたいっピ
わかりました。
他に知っておくべき公式は...
・円周 = 直径 × 3.14(π)
・側面積 = 底面の周 × 高さ
・円の面積 = 半径 × 半径 × 3.14(π)
ですね。
練習問題
(1)次の円柱の体積と表面積を求めなさい。ただし、円周率はπとする。

A. 体積...32π($cm^3$)・表面積...40π($cm^2$)
円柱の体積の求め方は「底面積 × 高さ」でしたね。
また円の求め方は「半径 × 半径 × π」なので、式は
2 × 2 × π × 8 = 32π
体積は32π($cm^3$)となります。
次に、円柱の表面積の求め方は「底面積 × 2 + 側面積」なので、式は「4π × 2 + 側面積」。
また、円柱の側面積の求め方は「高さ × 円周」、円周の求め方は「直径 × π」なので、式にすると 4π × 2 + 8 × 4π = 40π
なので、表面積は 40π($cm^2$)となります。
(2)次の三角柱の体積と表面積を求めなさい。
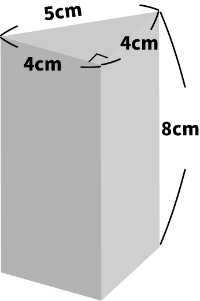
A. 体積...64($cm^3$)・表面積...120($cm^2$)
三角柱の体積の求め方は「底面積 × 高さ」でしたね。
底面積は $4×4×\frac{1}{2}=8$
よって、三角柱の体積は 8 × 8 = 64
体積は64($cm^3$)となります。
続いて、三角柱の表面積の公式は「底面積 × 2 + 側面積」でしたね。
すると、底面積は先に求めた$8cm^2$ですね。
側面積の求め方ですが「高さ × 底面の周の長さ」で求めることができます。
底面の周の長さは「5cm,4cm,4cm」と出ているので足して13cm。
なので、側面積は13 × 8 = 104
よって、三角柱の表面積は 8 × 2 + 104 = 120
表面積は120($cm^2$)となります。
2. 「錐」の体積・表面積の公式

四角錐

三角錐

円錐
錐の体積 = 底面積 × 高さ × ${\frac{1}{3}}$
四角錐・三角錐の表面積 = 底面積 + 側面積
円錐の表面積 = 半径 × π ×(半径 + 母線)
「母線」って何ピヨ?
母線は円錐のこの赤色の部分のことです!

練習問題
(1)次の円錐の体積と表面積を求めなさい。ただし、円周率はπとする。
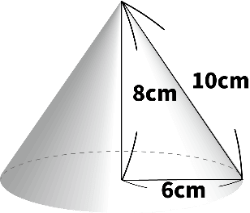
A. 体積...96π($cm^3$)・表面積...96π($cm^2$)
円錐の体積の公式は「底面積 × 高さ × $\frac{1}{3}$」でしたね。
よって、式は $6×6×π×8×\frac{1}{3}=96π$
円錐の体積は、96($cm^3$)となります。
続いて表面積です。
円錐の表面積の公式は「底面積 + 側面積」でしたね。
底面積は6 × 6 × π = 36π とすぐに出せますね。
続いて、円錐の側面積の求め方は「半径 × π(半径 + 母線)」でしたね。
よって、側面積の式は 6π(6 + 10)= 96π となります。
最後に底面積36πと側面積96πを足して、答えは132π($cm^2$)となります。
(2)次の三角錐の体積と表面積を求めなさい。ただし、∠BCD=90°、三角形ABDの高さを8cm、三角形ABCの高さを10cm、三角形ACDの高さを6cmとする。
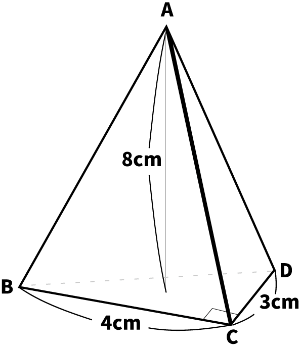
A. 体積...16($cm^3$)・表面積...55($cm^2$)
三角錐の体積の公式は「底面積 × 高さ × $\frac{1}{3}$」でしたね。
なので、式は$3×4×\frac{1}{2}×8×\frac{1}{3}=16$
三角錐の体積は16($cm^3$)となります。
次に三角錐の表面積の求め方は「底面積 + 側面積」でしたね。
なのでまずは底面積を出して、あとは側面積をそれぞれ出して最後に全てを足してあげます。
まず底面積は$3×4×\frac{1}{2}=6$
また、それぞれの側面積ですが、
△ABC$=4×10×\frac{1}{2}=20$
△ABD$=5×8×\frac{1}{2}=20$
△ACD$=3×6×\frac{1}{2}=9$
よって三角錐の表面積は、6+20+20+9=55
答えは55($cm^2$)となります。
3. 「球」の体積・表面積の公式
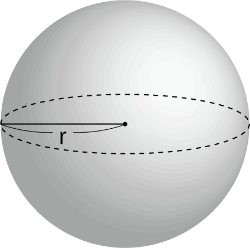
球
球の体積 = $\frac{4}{3}πr^3$
球の表面積 = $4πr^2$
この公式ほんと覚えられないピヨね...
よく言われている覚え方は、
・球の体積...3分の心配あーる参上
・球の表面積...心配あーる事情
という感じで語呂合わせで覚えるやつですね。
語呂合わせと気合いで覚えましょう。
練習問題
次の球の体積と表面積を求めなさい。ただし、円周率はπとする。
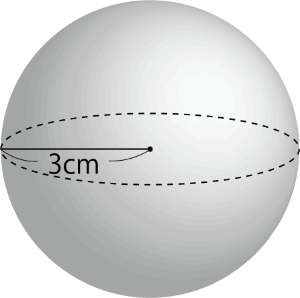
A. 体積...36π($cm^3$)・表面積...36π($cm^2$)
球の体積の求め方は$\frac{4}{3}πr^3$でしたね。
なので、式は$\frac{4}{3}π×3^3=36π$
よって、球の体積は36π($cm^3$)となります。
球の表面積の求め方は$4πr^2$でしたね。
なので、式は$4π×3^2=36π$
よって、球の表面積は36π($cm^2$)となります。
体積と表面積の求め方はわかったかな?
思ってたほど錐も柱もやることあまり変わらないピヨね。
そう!ただ、球だけは計算方法が全く異なるので、繰り返し解いて定着させましょう。
ピヨ!
あわせて読みたい
この記事を書いた人

元塾講師・元家庭教師
趣味はラジオを聴くこと
コーディングの勉強がてら
このサイトを作りました