【パターンの暗記で楽勝!】
三角形の合同の証明のやり方

高校受験に出題される合同の証明問題は、まず間違いなく三角形の合同の証明です。
三角形の合同の証明の「パターン」をしっかりおさえることが、証明問題を解くことのポイントになります。
1. 合同条件を覚えよう!
まずおさえておかなければいけないのは三角形の合同条件です!
「この条件が揃えば合同だよー」
という条件の組み合わせのことですね。これは覚えなければいけません!
えー...、暗記...。
...大丈夫です。覚えなければいけないのはたった5つだけなんです!
なっ!なんとっ!!
1-1. 三角形の合同条件
2つの三角形は、次のうちどれかに当てはまれば合同です。
① 3組の辺が、それぞれ等しい。
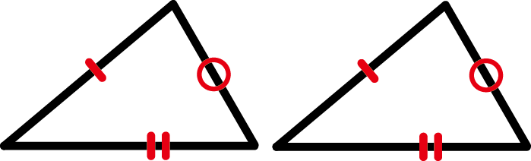
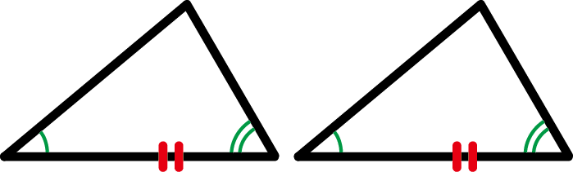
② 2組の辺とその間の角が、それぞれ等しい。
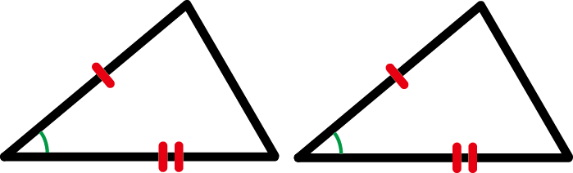
③ 1組の辺とその両端の角が、それぞれ等しい。
1-2. 直角三角形の合同条件
2つの直角三角形は、次のうちどれかに当てはまれば合同です。
④ 斜辺と1つの鋭角が、それぞれ等しい。

⑤ 斜辺と他の1辺が、それぞれ等しい。

ということで上記の5つだけは覚えておいてください!
やっぱり5つも覚えるのはきついピヨ...。
...困りましたね。そんなに暗記が嫌いですか。でも気持ちはわかります。
もし、本当に覚えるのが厳しかったら、とりあえず覚えるのは②と③だけでOKです!
では実際に、この合同条件を使って、どのように問題を解けば良いのでしょうか。
2. 必ず穴埋め問題から解け!
証明問題には大きく分けて2種類
・穴埋め問題
・完全証明
があります。
完全証明は、証明を丸ごと解答用紙に書いていくことになるので、ハードルが高いと感じる子が多いみたいですね。
実際の試験問題も「穴埋め問題」の方が簡単になっていることが多いみたいです。
ということで、テストの時は「穴埋め問題」の方から解いていくようにしましょう!
それでは、まず「穴埋め問題」の解き方から解説していきます。
2-1. 【同じ長さ】【同じ角度】を見つけよう!
まずは、こちらの問題をご覧ください。
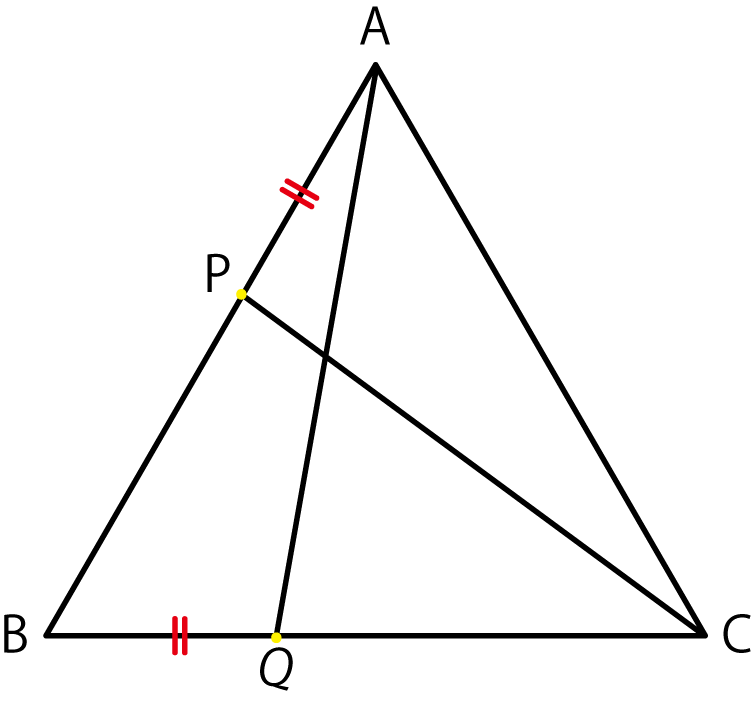
△ABCは正三角形、P、Qはそれぞれ辺AB、BC上の点で、AP=BQである。
この時、角BAQ=角ACPであることを次のように証明した。【 】をうめて証明を完成させなさい。
【証明】
△ABQと△CAPにおいて、△ABCは正三角形だから、
AB=【 (1) 】・・・①
角ABQ=【 (2) 】=60°・・・②
また、BQ=AP・・・③
①、②、③から、【 (3) 】がそれぞれ等しいので、
△ABQ ≡ △CAP
よって、角BAQ=角ACP
一見難しそうですね。
ただご安心ください。証明の穴埋め問題は、思ってるよりも簡単に解けます。
試験に出てきたら、次のことを意識してチャレンジしてみてください。
大事なのは、証明の一文目
「△ABQと△CAPにおいて」
です!
二つの三角形が図で言うとどこを表しているのかを必ず確認してください。
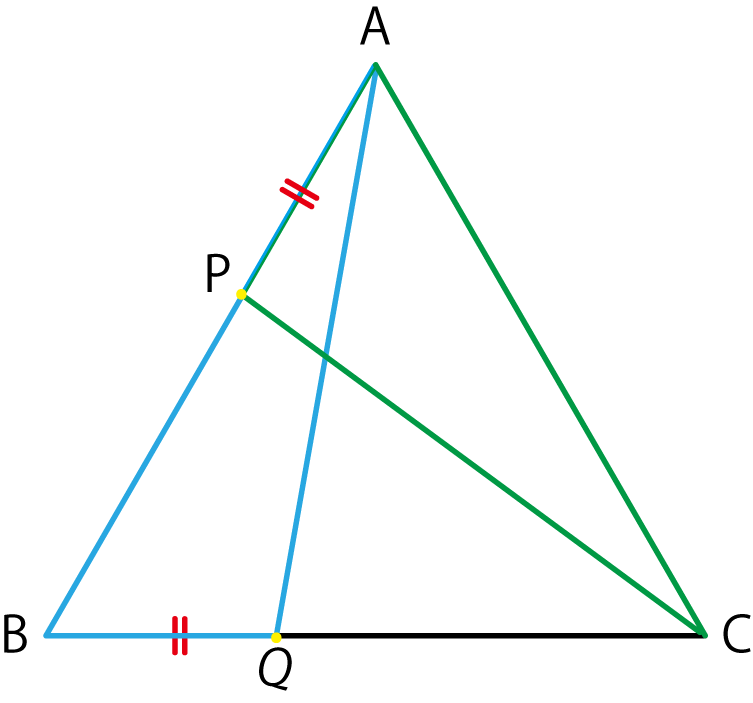
合同に関しては、この二つの三角形だけに注目すればいいことがわかります。
二つの三角形に注目しながら、空欄を埋めていきましょう。
まず、
「AB=【 (1) 】・・・①」
こちらですが、まずABは、△ABQ上の一辺です。
ABと同じ長さの辺を△CAP上から見つけていきます。
正三角形の性質を使うことが、証明中のヒントとして書いてありますね。ABは正三角形△ABCの中の一辺でもあります。
△CAPの中で、正三角形の辺にもなっているのは辺CAですね
と言うことで、
「AB=CA・・・①」
が正解になります。
同じように、
「角ABQ=【 (2) 】=60°・・・②」
こちらですが、60°からわかるように、正三角形の一つの角の大きさを利用します。
角ABQは△ABQの中の角です。対する、△CAPの中で、正三角形の角にもなっている角を見つけます。これは、角CAPになりますね。
「角ABQ=角CAP=60°・・・②」
2-2. 合同条件はほぼ2択!
次に、【 (3) 】をうめていきます。
ここには、三角形の合同条件を入れます。ここがしっかり答えられるようにするために、三角形の合同条件を暗記するんですね。
実は、ここに入る合同条件は、ほとんどの場合
② 2組の辺とその間の角が、それぞれ等しい。
③ 1組の辺とその両端の角が、それぞれ等しい。
のどちらかなんです!
ここで、①〜③の条件を一度並べてみましょう。
AB=CA・・・①
角ABQ=角CAP=60°・・・②
BQ=AP・・・③
条件の中に、「辺の長さ」に関する条件がいくつあるか数えてみましょう。
・・・
これは...、①と③ピヨ!
大正解!
この時点で、使用する条件は「② 2組の辺とその間の角が、それぞれ等しい。」であることがわかります。
図を確認すると、②の条件の角が①、③の条件の辺にそれぞれ挟まれている(「間の角」になっている)ことがわかりますね。
と言うことで、文章に合うように空欄をうめるとすれば、
①、②、③から、【2組の辺とその間の角】がそれぞれ等しいので
となります。
実は、穴埋め問題は意外に簡単に解ける問題が多いです。
忘れないうちに、試しにワークなどで実践してみてください。
〜ここまでのまとめ〜
① 【同じ長さ】【同じ角度】を見つける。
② 合同条件を選ぶ(ほぼ2択)
3. 完全証明も穴埋め!
では、この流れでもう1問いってみましょう!
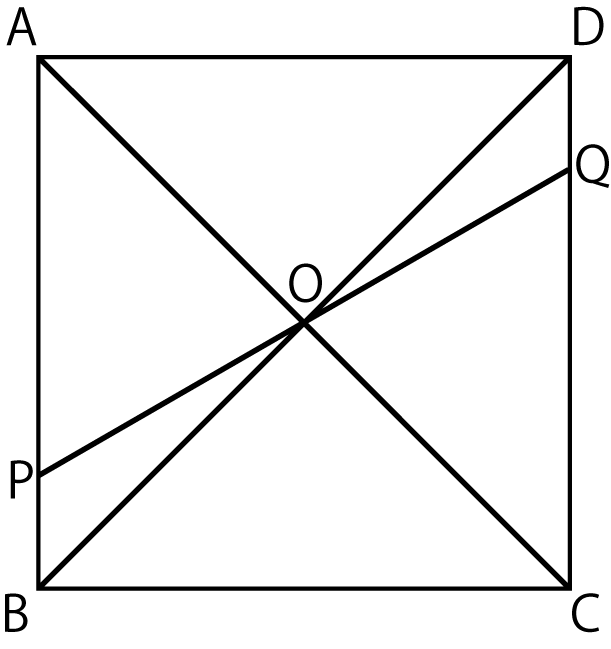
上の図のように、正方形ABCDの対角線の交点をOとし、辺AB上にA、Bと異なるPをとる。
直線POと辺CDの交点をQとするとき、△BOP ≡ △DOQであることを証明せよ。
次は、このような完全証明の問題の解き方を解説していきます。
ここでのポイントは、完全証明はテンプレートにそって解くことです。
決して、自由作文のように考えてはいけません。

合同の完全証明でも、このようにテンプレートへ穴埋めをする形でとけば大したことありません!
まずは、問題文に対象とする三角形が書いてあるので、そこをうめていきます。

これでひとまず下準備は完了です。次から「合同条件」をうめていきます。
3-1. 合同条件はほぼ2択!
先ほど穴埋めに書き込んだ三角形「△BOP」と「△DOQ」をよくみて、その中に「同じ長さ」「同じ角度」を見つけていきましょう。
まずは、下の図のように、図形の中に「同じ長さ」「同じ角度」に印をつけていきます。
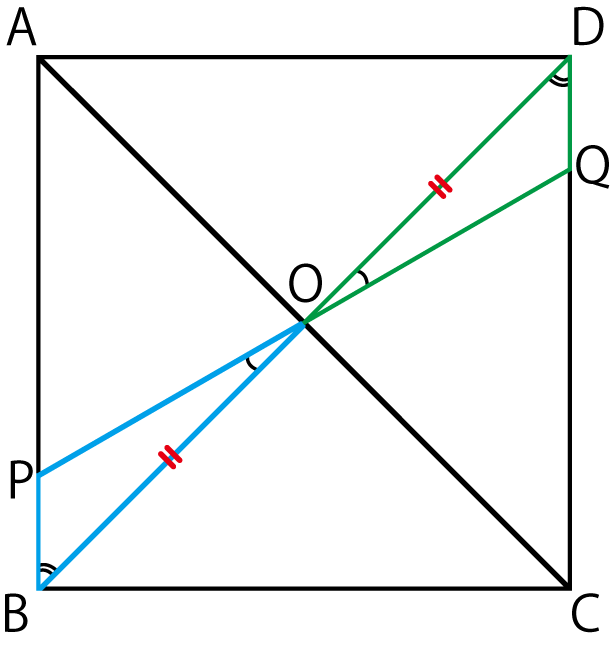
そしたら次に、五つの合同条件のどれかに沿うものを探していきます。
(...合同条件ど忘れしちゃっピー..)
そしたら、下のボタンを押してもう一度確認してみてください!
① 3組の辺が、それぞれ等しい。

② 2組の辺とその間の角が、それぞれ等しい。

③ 1組の辺とその両端の角が、それぞれ等しい。

④ 斜辺と1つの鋭角が、それぞれ等しい。

⑤ 斜辺と他の1辺が、それぞれ等しい。

五つの合同条件に沿うものは見つけられましたか?
実は完全証明の場合も、大体の場合が合同条件②か③です。
図で確認すると、「同じ長さの辺が1組」「その両端に同じ角度」がありますね。
と言うことで合同条件③の1組の辺とその両端の角が、それぞれ等しい。
であることがわかりました。
これのことか!

そうです!
それでは、先ほどのテンプレートへ、合同条件を書きましょう。

3-2. 根拠を必ず書け!
完全証明で難しいのがなぜ等しいのかの根拠が必要なところです。
図をみながら根拠を見つけていきましょう。

まずは「BO = DO」です。
これは「平行四辺形の対角線が、それぞれ中点で交わる」ことを知ってなければいけません。
正方形も平行四辺形と性質は同じなので、テンプレートの空欄へは「正方形の対角線は中点で交わるから」と書きましょう。
次に「角BOP = 角DOQ」ですが、これは対頂角が等しいことがわかっていれば大丈夫ですね。
テンプレートへはこのように書きましょう。
「対頂角は等しいから、角BOP = 角DOQ」
最後に「角PBO = 角QDO」ですが、これも正方形の性質(平行四辺形の性質)を使います。
向かい合う辺ABと辺CDが平行になっていることを使いましょう。
平行線で同じ角度といえば、、、?
...錯角?
そうです!よくできました!
空欄へはこう書きましょう。
AB//CDより錯角は等しいから、角PBO = 角QDO
これで証明が完成ですね。
完成した証明がこちらです。

以上が、証明問題(三角形の合同)の解き方の基本になります。
ちょっと分かってきた気がするピヨ!
ただ、今分かってても実際に問題を繰り返し解いて、使いこなせるようにしてくださいね!
分かったピヨ!
何度も繰り返し解いてると
「あれ?証明簡単...」
と感じる瞬間がきます。
ぜひ皆さんも、上記のやり方をぜひ試してみてください!
あわせて読みたい
この記事を書いた人

元塾講師・元家庭教師
趣味はラジオを聴くこと
コーディングの勉強がてら
このサイトを作りました