【中学数学】確率問題の解き方(サイコロ・トランプ・カード・硬貨・玉を取り出すなど)
袋から玉を取り出して、戻して...あーー!もうわからないピヨーー!
確率問題ですね。苦手な子が非常に多い分野です。
教えて欲しいピヨ...。
わかりました。教えてあげましょう!
トランプ問題の解き方
まずはこの問題から一緒に解いていきましょう!
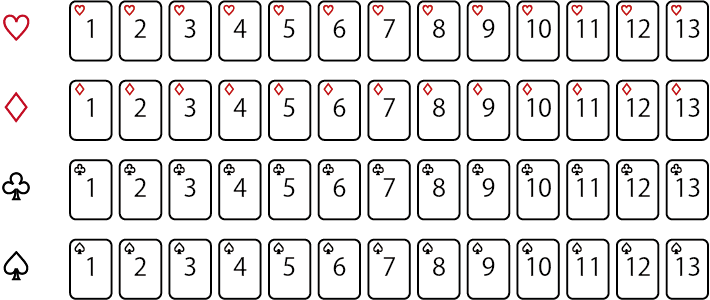
ジョーカーを除く1組(52枚)のトランプから、1枚のカードを引く時、次の問いに答えなさい。
(1)取り出したカードが「ハートのA(エース)」である確率を求めなさい。
(2)取り出したカードが「A(エース)」である確率を求めなさい。
解き方はとってもシンプルです!
以下のステップで解けちゃいます!
① 分母(全体の場合の数)を求める
② 分子(求める事柄の場合の数)を求める
③ 約分する
まず、分母となる「全体の場合の数」を出します。
トランプは、ジョーカーを除くと全部で「52枚」なので、分母は「52」になります。

続いて、(1)の分子(求める事柄の場合の数)を求めていきます。
52枚のトランプのなかで「ハートのエース」は何枚あるかというと、
1枚ピヨね!

なので、分子(求める事柄の場合の数)は「1」となります。
最後に約分なんですが...
今回だと$\Large{\frac{1}{52}}$と約分ができませんので、これがそのまま答えとなります。
続いて、(2)です。取り出したカードが「A(エース)」である確率です。
52枚のトランプの中でA(エース)は何枚あるかというと、

全部で4枚ですね。
分母は最初に出した「52」なので、$\Large{\frac{4}{52}}$となり、約分した最終的な答えは「$\Large{\frac{1}{13}}$」となります。
意外と簡単ピヨね
2つのサイコロ問題の解き方
お次はサイコロ問題です!

2つのサイコロを同時に投げるとき、
次の確率を求めなさい。
(1)出た目の和が10になる確率
(2)3の目がでない確率
(3)出た目の差が2になる確率
(4)少なくともどちらか一方が3以上になる確率
中学校の確率問題では「二つのサイコロを振る」問題はたくさん出てきます。
この手の問題の解き方も3つのステップで解けちゃいます!
① 分母(全体の場合の数)を求める
② 分子(求める事柄の場合の数)を求める
③ 約分する
まずは分母(全体の場合の数)から求めていきます。
サイコロの目は「6つ」ありますね。
そのサイコロを2つ投げるわけなので、全体の場合の数は次のように考えることができます。(区別をするためにそれぞれ「サイコロA」と「サイコロB」とします)
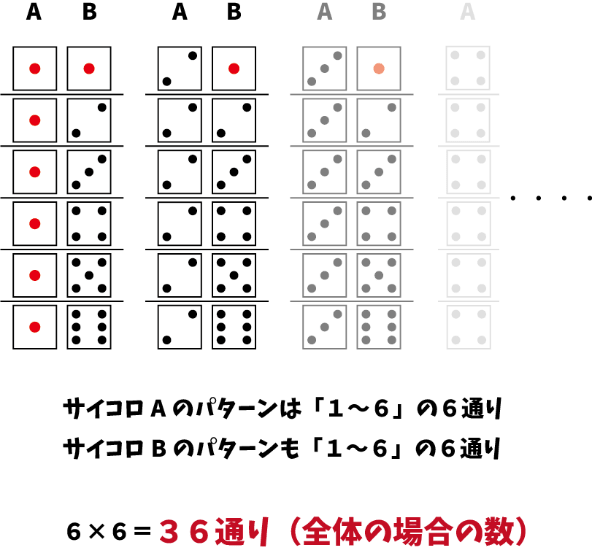
となり、まずは分母(全体の場合の数)が求められました!
「2つのサイコロを振る」ときの目の出方は「全部で36通り」というのはそのまま暗記しちゃいましょう。
それでは各問題を解いていきます。
(1)出た目の和が10になる確率
サイコロの和が10になる出方は何があるかな?
ん〜、(4,6)(5,5)(6,4)の3通りピヨ!
その通り!
式にすると$\Large{\frac{3}{36}}$となります。約分すると答えは$\Large{\frac{1}{12}}$となります。
(2)3の目がでない確率
まず、全体の場合の数(ここでは36)から「3が出る場合の数」を引いてあげます!
「〇〇が出ない場合の数」=「全体の場合の数」ー「〇〇が出る場合の数」
これにしたがって、3の目が一つでも入る組み合わせを書き出して、場合の数をだすとこうなります。

あとは、全体の場合の数から少なくとも3が出る場合の数を引いてあげます。

これで「3がでない場合の数」を出すことができました。
よって答えは「$\Large{\frac{25}{36}}$」となります。
(3)でた目の差が2になる確率
まずは、出た目の差が2になる組み合わせを書き出してみましょう。

これで「出た目の差が2になる場合の数」が出ました。
あとは、分母を「36」にして分数にすると
$\Large{\frac{8}{36}}$
約分して、答えは$\Large{\frac{2}{9}}$となります
(4)少なくとも一方は3以上になる確率
サイコロの目で3以上のものは「3,4,5,6」の4つです。
ということは、3未満の目は「1,2」の2つだけなので、考え方としてはこうなります。
「全体の場合の数」ー「3未満の目が出る場合の数」
=「3以上の目がでる場合の数」
3未満の目が出る組み合わせは何があるかな?
ん〜、(1,1)(1,2)(2,1)(2,2)の4つピヨ!
そうなりますね!
したがって、36-4=32(少なくとも一方が3以上になる場合の数)となります。
よって、少なくとも一方が3以上になる確率は「$\Large{\frac{32}{36}}$」。約分して、答えは$\Large{\frac{8}{9}}$となります。
カードで整数作る問題の解き方
整数問題は非常に簡単です!
1〜5の数字が書かれたカードを連続で2枚取ります。
1枚目を十の位、2枚目を一の位として2けたの整数を作るとき、
次の確率を求めなさい。
(1)整数が3の倍数になる確率を求めなさい。
(2)整数が30以上になる確率を求めなさい。
まずは「全ての場合の数」から求めていきます。
ここでは樹形図を使います!
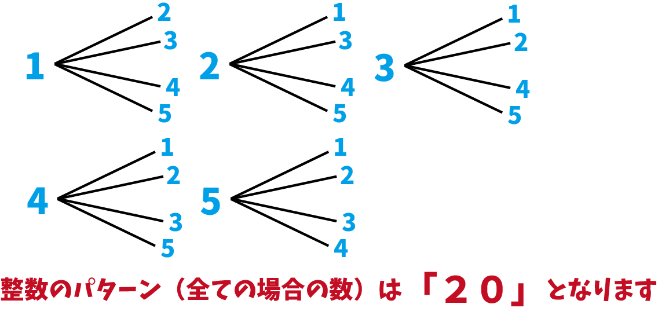
分母が出たので次に各問題の解き方を説明していきます。
(1)整数が3の倍数になる確率
3の倍数になる整数を樹形図で探していきます。
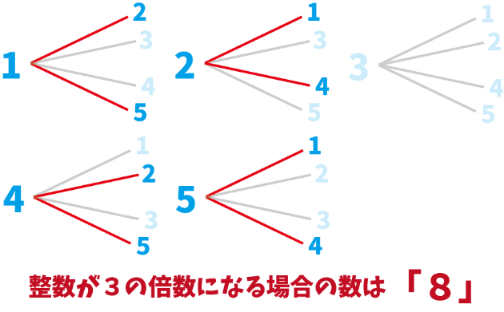
全部で8パターンピヨね!
と言うことで、「整数が3の倍数になる確率」は$\Large{\frac{8}{20}}$で、約分すると答えは$\Large{\frac{2}{5}}$となります。
(1)整数が30以上になる確率
「整数が30以上」と言うことは、「10の位が3以上」だと言うことです。
なので樹形図で考えるとこうなります。

なので、整数が30以上になる確率は$\Large{\frac{12}{30}}$、約分して答えは$\Large{\frac{2}{5}}$となります。
袋から玉を取り出す問題の解き方

赤玉4個と青玉3個が入っている袋があります。
この袋から玉を1個取り出して色を確認し袋に戻します。
戻したらまたもう一度袋から玉を取り出すとき、次の確率を求めなさい。
(1)赤玉と青玉が出る確率
(2)同じ色の玉が出る確率
「1回戻す」やつが苦手ピヨ...。
実は考え方は「2つのサイコロ」問題と非常によく似ています。
まず、全体の場合の数を出していきます。
サイコロを2つ振る場合の出る目の組み合わせは、「6×6=36通り」という計算をしましたね。
これと考え方は全く一緒です。今回、袋の中には「7つ」玉が入ってます。なので、玉の出方は7通りですね。
玉を取ったら袋に戻してしまうので、2回目に玉を取るときの玉の出方も7通りです。
なので、全体の場合の数は「7×7=49」となります。
それでは(1)と(2)を順番に解いていきましょう。
(1)赤玉と青玉が出る確率
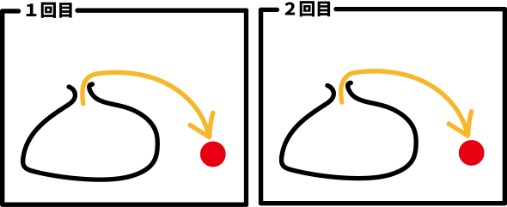
まず前提として、全ての玉は区別して考えなければいけません。
赤玉4つはそれぞれ別物、青玉3つは全て別物ということです。
なので、まずは玉に数字を振って(こんな感じで)

区別してあげましょう。
今回求めたいのは、「赤玉と青玉が出る確率」なので、まずは、
・1回目に赤玉、2回目に青玉が出る場合の数
・1回目に青玉、2回目に赤玉が出る確率
をそれぞれ求めていきます。
まず、場合の数ですね。
合計で2回取り出しますが、取り出すたびに袋に戻しているので、取り出し方の場合の数は「7×7=49通り」となります。
その上で、「1回目に青玉、2回目に赤玉が出る場合の数」を計算してみると、
赤玉→青玉:4×3=12通り
青玉→赤玉:3×4=12通り
ということで、赤玉と青玉がでる場合の数は「24通り」となります。
よって、(1)の答えは$\Large{\frac{24}{49}}$
(2)同じ色の玉が出る確率
続いて、(2)の「同じ玉が出る確率」を求めていきます。
解き方の手順は「1回目に赤玉、2回目も赤玉」「1回目に青玉、2回目も青玉」が出る確率をそれぞれ出して、最後に足すという流れです。
「1回目に赤玉、2回目も赤玉」が出る確率は、$\Large{\frac{4}{7}×\frac{4}{7}=\frac{16}{49}}$
「1回目に青玉、2回目も青玉」が出る確率は、$\Large{\frac{3}{7}×\frac{3}{7}=\frac{9}{49}}$
それぞれの答えを足すと、
$\Large{\frac{16}{49}+\frac{9}{49}=\frac{25}{49}}$
(2)の答えは$\Large{\frac{25}{49}}$
硬貨問題の解き方

500円、100円、50円、10円の硬貨が1枚ずつあります。この4枚を同時に投げるとき、次の問いに答えなさい。
(1)表裏の出方は全部で何通りありますか。
(2)4枚のうち2枚以上が表になる確率を求めなさい。
(3)表がでた硬貨の合計金額が、530円以上になる確率を求めなさい。
硬貨の出方の問題ピヨね...
硬貨の問題は簡単ですよ!
(1)表裏の出方は何通りあるか
硬貨は全部で4枚あります。一枚ずつで考えると表と裏で2通りの出方があります。
これが4枚あると次のようになります。

上の図からわかるように、式にするなら
$\Large{2×2×2×2=2^4=16}$通り
となります。
これが、(1)の答えになりますね。
(2)4枚のうち2枚以上が表になる確率
「2枚以上が表になる確率」の求める手順はこうです。
① 表が1枚しかでない確率を求める
② 表が一枚も出ない確率を求める
③ ①と②の和を全体の場合の数から引く
となります。
つまり、「2枚以上が表になる確率」を求めにいくというより、2枚以上が表になる場合"以外"を考えます。
まず手順①の「表は1枚しか出ないパターン」は全部で4通り(表裏裏裏・裏表裏裏・裏裏表裏・裏裏裏表)あります。
確率にすると$\Large{\frac{4}{16}}$
次に、手順②の「表が1枚も出ないパターン」は1通り(裏裏裏裏)ですね。
確率にすると$\Large{\frac{1}{16}}$
最後に全体の場合の数から①と②の和を引いてあげます。
$\Large{\frac{16}{16}-(\frac{4}{16}+\frac{1}{16})=\frac{11}{16}}$
4枚のうち2枚以上が表になる確率は$\Large{\frac{11}{16}}$となります。
(3)表がでた硬貨の合計が530円以上になる確率
これは、まず530円以上になる硬貨の組み合わせを書き出していきましょう。
500+100+50+10=660円
500+100+50=650円
500+100+10=610円
500+100=600円
500+50+10=560円
500+50=550円
この6通りが、530円以上になる組み合わせになります。
よって、$\Large{\frac{6}{16}=\frac{3}{8}}$となります
いかがでしたか?
確率問題っていろいろな種類があると思ってしまいそうですが、実際にはほとんどやってることは同じです。
分数の分母に「全体の場合の数」を当てはめて、分子に「求めなくてはならない場合の数」当てはめて、最後に約分して〜といったように。
今このページを読んでいる方が、わからなかった確率の問題を改めて解き直してみてください。
スラスラ解けるようになってるはずです!
あわせて読みたい
この記事を書いた人

元塾講師・元家庭教師
趣味はラジオを聴くこと
コーディングの勉強がてら
このサイトを作りました