【中1数学】データの活用を理解しよう!(度数分布表・ヒストグラム・代表値・相対度数)
ヒストグラムの問題、全然解けないピヨ
そうだね。難しく感じてる子が多い単元ですね。
階級値...?相対度数...?何が何だかピヨー!
大丈夫!この単元、実は超簡単なのに対策が後回しにされがちな分野だから、お買い得分野なのです!
それは、絶対にマスターしたいピヨ!!!!
中1の数学の最終単元が「データの活用」です。
学校の授業でも、時間が足りなくなって大急ぎで学習することになってしまった...という声をよく聞きます。
他の単元に比べて覚える用語は多いですが、問題を解くのは超簡単です!
難しい問題を作るには限界のある分野なので、絶対押さえておきましょう!
では参ります!
1. データの活用で学習する内容
中1の数学で習う「データの活用」を学習すると、
ことができるようになります。
データ分析のやり方を知っておくととても便利なので、今のうちにマスターしちゃいましょう!
2. 出てくる用語の意味と使い方
とあるデータ
ある男子生徒20人の体重を測ったところ、以下のような記録になりました。
42,51,48,55,41,50,48,44,49,60,
56,37,47,52,55,45,40,61,43,48
(単位...kg)
この「とあるデータ」を元に必須用語の意味や使い方を解説していきます!
最大値・最小値・範囲
最大値...データの値の中で、もっとも大きい値
最小値...データの値の中で、もっとも小さい値
範囲...最大値と最小値の差
※範囲を求める式は「範囲=最大値ー最小値」と表せます。
それでは、以下の「とあるデータ」をみながら「最大値」「最小値」「範囲」を求めてみましょう!
ある男子生徒20人の体重を測ったところ、以下のような記録になりました。
42,51,48,55,41,50,48,44,49,60,
56,37,47,52,55,45,40,61,43,48
(単位...kg)
わかりましたか?
できたピヨ!
それでは正解をみてみましょう!
最大値...61(kg)
42,51,48,55,41,50,48,44,49,60,
56,37,47,52,55,45,40,61,43,48
(単位...kg)
最小値...37(kg)
42,51,48,55,41,50,48,44,49,60,
56,37,47,52,55,45,40,61,43,48
(単位...kg)
範囲...24(kg)
※式)61-37=24
度数分布表(度数と階級)
度数分布表とは、数字のデータを階級ごとに整理して表にしたものです。
まずは、「とあるデータ」を度数分布表にしていきましょう。
| 体重の記録 | |
|---|---|
| 階級(kg) | 度数(人) |
| 以上 未満 | |
| 34 〜 40 | |
| 40 〜 46 | |
| 46 〜 52 | |
| 52 〜 58 | |
| 58 〜 64 | |
| 計 | 20 |
ある男子生徒20人の体重を測ったところ、以下のような記録になりました。
42,51,48,55,41,50,48,44,49,60,
56,37,47,52,55,45,40,61,43,48
(単位...kg)
こんなの感じの表ピヨか...。
ところで、階級と度数ってどういう意味ピヨ?
上でやったように、データを整理した1つ1つの区間を「階級」と言います。
※ボクシングの階級をイメージするとわかりやすいかも!
また、各階級に入るデータの個数を、その階級の「度数」と言います。
では、「とあるデータ」を度数分布表に書き入れていきます!
| 体重の記録 | |
|---|---|
| 階級(kg) | 度数(人) |
| 以上 未満 | |
| 34 〜 40 | |
| 40 〜 46 | |
| 46 〜 52 | |
| 52 〜 58 | |
| 58 〜 64 | |
| 計 | 20 |
まず、体重が34kg以上40kg未満の生徒は、全体の中で1人だけですね!
ある男子生徒20人の体重を測ったところ、以下のような記録になりました。
42,51,48,55,41,50,48,44,49,60,
56,37,47,52,55,45,40,61,43,48
(単位...kg)
ということは、34kg以上40kg未満の階級の度数は1(人)ってことピヨか!
そういうこと!
度数分布表に埋めていくと...
| 体重の記録 | |
|---|---|
| 階級(kg) | 度数(人) |
| 以上 未満 | |
| 34 〜 40 | 1 |
| 40 〜 46 | |
| 46 〜 52 | |
| 52 〜 58 | |
| 58 〜 64 | |
| 計 | 20 |
こんな感じになります!
では次に、40kg以上46kg未満の階級の度数ですが、いくつだと思いますか?
ええと、全部で6人ピヨ!
ある男子生徒20人の体重を測ったところ、以下のような記録になりました。
42,51,48,55,41,50,48,44,49,60,
56,37,47,52,55,45,40,61,43,48
(単位...kg)
度数分布表に埋めていくと...
| 体重の記録 | |
|---|---|
| 階級(kg) | 度数(人) |
| 以上 未満 | |
| 34 〜 40 | 1 |
| 40 〜 46 | 6 |
| 46 〜 52 | |
| 52 〜 58 | |
| 58 〜 64 | |
| 計 | 20 |
こんな感じで、残りの階級も全て埋めていくと...
| 体重の記録 | |
|---|---|
| 階級(kg) | 度数(人) |
| 以上 未満 | |
| 34 〜 40 | 1 |
| 40 〜 46 | 6 |
| 46 〜 52 | 7 |
| 52 〜 58 | 4 |
| 58 〜 64 | 2 |
| 計 | 20 |
こんな感じになります。
これで、度数分布表が完成しました!
ヒストグラムと書き方
ヒストグラムとは、わかりやすくいうと「棒グラフ」みたいなものです。
データを棒のグラフにしたものです。
見た目は棒グラフとほとんど変わりませんが、棒グラフとヒストグラムでは用いられる用途が異なります。
棒グラフ...データどうし(棒どうし)を比較する用途
ヒストグラム...グラフ全体をみて、数値の分布(偏り)をみる(どの辺に数値が集中してるな〜みたいな)。
それでは実際に「とあるデータ」のヒストグラムを作成していきます!
以下に先程の度数分布表がありますので、そちらにグラフを入れていきます。
| 体重の記録 | |
|---|---|
| 階級(kg) | 度数(人) |
| 以上 未満 | |
| 34 〜 40 | 1 |
| 40 〜 46 | 6 |
| 46 〜 52 | 7 |
| 52 〜 58 | 4 |
| 58 〜 64 | 2 |
| 計 | 20 |
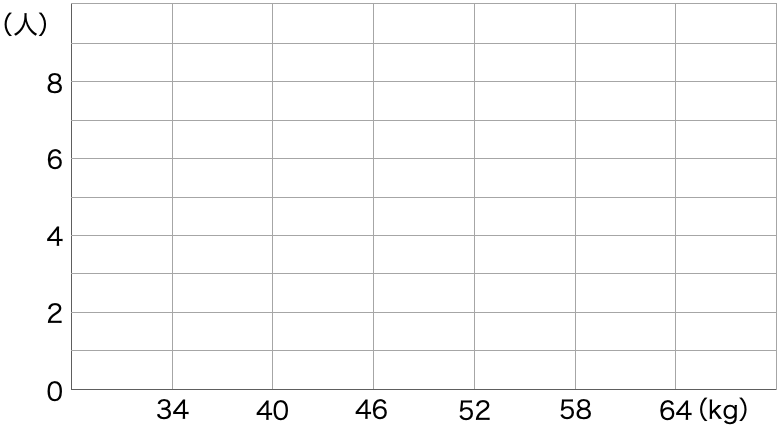
完成したヒストグラムはこんな感じ!
思ってたより全然簡単ピヨね!
そう!意外に簡単なんです!
ちなみに、完成したヒストグラムをみてみると、40kg以上52kg未満の人数(度数)が多くなっていることがわかりますね。
これがヒストグラムです。
度数分布多角形
なんかまた難しそうな言葉が出てきたピヨ...
ひよこくん。ご安心を...。
度数分布多角形は正直ヒストグラムよりも簡単です!
度数分布多角形とは...ヒストグラムを折れ線グラフにしたもの。
書き方は超簡単!
① ヒストグラムの1つ1つのデータの上辺の真ん中に点を打つ
② 両端は度数0の階級があるものとするので、0に点を打つ
③ 点どうしを線で結ぶ
え、、、これだけピヨ?
これならすぐにかけそうピヨ!
では、ヒストグラムに度数分布多角形を記入していきましょう!
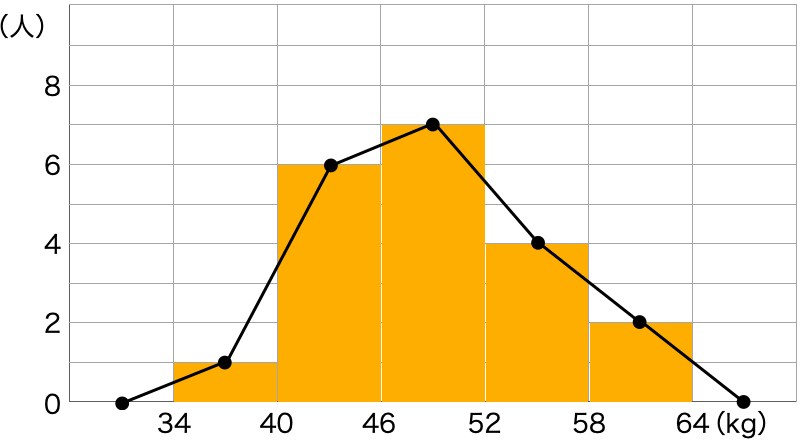
このような度数分布多角形が完成します!
3. 代表値と相対度数
ここからは、代表値と相対度数について解説していきます!
相対度数は苦手ピヨ...。
いつもよくわからなくなっちゃうっピ...。
大丈夫!そんなに難しくはないので、すぐにマスターできますよ!
代表値(平均値・中央値・最頻値)
代表値は、簡単にいうと「データの中ですごく大事な数値」のこと。
また、代表値には大きく分けて3種類の値があります。
① 平均値...データ全体の平均の値
平均値の求め方...$\Large{\frac{\rm{値の合計}}{\rm{資料の個数}}}$
② 中央値(メジアン)...データを大きさ順に並べた時にちょうど中央に来る値
③ 最頻値(モード)...データの中で一番多く出てくる値
では、「とあるデータ」から、平均値、中央値、最頻値を見つけていきます。
まずは、「とあるデータ」の数値を大きさ順に並び替えてみましょう!
ある男子生徒20人の体重を測ったところ、以下のような記録になりました。
37,40,41,42,43,44,45,47,48,48,
48,49,50,51,52,55,55,56,60,61
(単位...kg)
「とあるデータ」から、それぞれ代表値を求めてみると、
・平均値...48.6
・中央値...48
・最頻値...48
となります。
大きさ順に並べると代表値を見つけやすいっピ!
階級値
階級値とは...その階級の真ん中の値のこと!
例えば、34kg以上40kg未満の階級値は、$\Large{\frac{34+40}{2}=37}$
◯以上◯未満の数を足して2で割ると、その階級値が出るピヨね!
そう言うことです!
では、「とあるデータ」の階級値を求めてみましょう!
| 体重の記録 | ||
|---|---|---|
| 階級(kg) | 度数(人) | 階級値(kg) |
| 以上 未満 | ||
| 34 〜 40 | 1 | 37 |
| 40 〜 46 | 6 | 43 |
| 46 〜 52 | 7 | 49 |
| 52 〜 58 | 4 | 53 |
| 58 〜 64 | 2 | 61 |
| 計 | 20 | ー |
相対度数
【復習】度数とは...各階級に入るデータの個数のことを、その階級の「度数」と言います。
相対度数とは...全体の度数に対する各階級の度数の割合。
相対度数の求め方...$\Large{\frac{\rm{その階級の度数}}{\rm{度数の合計}}}$
例えばボクシングで言うと、「ボクシングのフライ級の人数って、全ボクシング競技者のうちのどれくらいの割合いるのか?」
こんなのを表す数値が相対度数です。
なるほどっピ!
それでは、「とあるデータ」の相対度数を求めていきましょう!
| 体重の記録 | ||
|---|---|---|
| 階級(kg) | 度数(人) | 相対度数 |
| 以上 未満 | ||
| 34 〜 40 | 1 | 0.05 |
| 40 〜 46 | 6 | 0.3 |
| 46 〜 52 | 7 | 0.35 |
| 52 〜 58 | 4 | 0.2 |
| 58 〜 64 | 2 | 0.1 |
| 計 | 20 | 1 |
相対度数は単純な計算で求めることができます!
累積相対度数
累積相対度数とは...相対度数を上の階級から足していった数値。
どういうことっピ?
では、以下の表をみてください。
| 体重の記録 | |||
|---|---|---|---|
| 階級(kg) | 相対度数 | 累積相対度数 | |
| 以上 未満 | |||
| 34 〜 40 | 0.05 | 0.05 | |
| 40 〜 46 | 0.3 | 0.35 | |
| 46 〜 52 | 0.35 | 0.7 | |
| 52 〜 58 | 0.2 | 0.9 | |
| 58 〜 64 | 0.1 | 1 | |
| 計 | 1 | ||
このように、相対度数の「累積」なので、相対度数を上の階級からどんどん足していくだけで、累積相対度数を求めることができます。
簡単ピヨね!
4. データにもとづく確率
データの活用について基本的な事項がわかったところで、次のステップに進みます。
データの活用を使った「確率問題」の解き方です。
確率だけでも難しいのに、データの活用が絡んでくると、やっかいだっピ...。
コインを投げるときの面の出方は?
【例題】
下の表は、コインAとBを何回も投げて、表と裏の出た回数をまとめたものです。
コインAとBでは、どちらの方が、表が出やすいと言えますか。
| コイン\出た面 | 表 | 裏 | 合計 |
|---|---|---|---|
| A | 1050 | 1450 | 2500 |
| B | 1380 | 1620 | 3000 |
さぁ、この問題。ひよこくんわかるかな?
コインふる回数が同じならわかりそうだけど、回数がこんなに違うとわからないっピ...。
大丈夫!こんな時に使えるのが、先ほど学習した「相対度数」です!
【復習】度数とは...各階級に入るデータの個数のことを、その階級の「度数」と言います。
【復習】相対度数とは...全体の度数に対する各階級の度数の割合。
相対度数の求め方...$\Large{\frac{\rm{その階級の度数}}{\rm{度数の合計}}}$
ってことは、表が出る場合の相対度数が高い方が答えになるってことっピ?
お見事!
うピョー!!
では、これを踏まえてもう一度問題をみてみましょう。
【例題】
下の表は、コインAとBを何回も投げて、表と裏の出た回数をまとめたものです。
コインAとBでは、どちらの方が、表が出やすいと言えますか。
| コイン\出た面 | 表 | 裏 | 合計 |
|---|---|---|---|
| A | 1050 | 1450 | 2500 |
| B | 1380 | 1620 | 3000 |
それぞれの相対度数を出してみると...
| コイン(A) | コイン(B) | ||
|---|---|---|---|
| コインの出た面 | 相対度数 | コインの出た面 | 相対度数 |
| 表 | 0.42 | 表 | 0.46 |
| 裏 | 0.58 | 裏 | 0.54 |
表が出る場合の相対度数はコイン(B)の方が大きいことがわかります。
よって、コイン(B)の方が表が出やすいと言うことができます。
なるほどっピ!
今回は中学1年生で習う「データの活用」をやりました。
しっかり復習しましょうね。
わかったピヨ!
あわせて読みたい
この記事を書いた人

元塾講師・元家庭教師
趣味はラジオを聴くこと
コーディングの勉強がてら
このサイトを作りました